Solutions

 

1. Define complexity? Explain Time & Space Complexity.

Answer: Complexity of an algorithm is a measure of the amount of time and/or space required by an algorithm for an input of a given size (n).  

Algorithm complexity is a measure which evaluates the order of the count of operations, performed by a given or algorithm as a function of the size of the input data. In simple words, complexity is a rough approximation of the number of steps necessary to execute an algorithm. Complexity can be constant, logarithmic, linear, n*log(n), quadratic, cubic, exponential, etc. This is respectively the order of constant, logarithmic, linear and so on, number of steps, are executed to solve a given problem.

The complexity of an algorithm can be divided into two types. The time complexity and the space complexity.

Time Complexity:

• The time needed by an algorithm expressed as a function of the size of a problem is called the TIME COMPLEXITY of the algorithm. The time complexity of a program is the amount of computer time it needs to run to completion.
• The limiting behavior of the complexity as size increases is called the asymptotic time complexity. It is the asymptotic complexity of an algorithm, which ultimately determines the size of problems that can be solved by the algorithm.
• Generally, running time of an algorithm depends upon the following: 
• Whether it is running on Single processor machine or Multiprocessor machine. 
• Whether it is a 32-bit machine or 64-bit machine.
• Read and Write speed of the machine. 
• The time it takes to perform Arithmetic operations, logical operations, return value and assignment operations etc. 
• Input data

Space Complexity: 

• The space complexity of a program is the amount of memory it needs to run to completion. The space need by a program has the following components:  
• Instruction space: Instruction space is the space needed to store the compiled version of the program instructions. 
• Data space: Data space is the space needed to store all constant and variable values. Data space has two components:  
• Space needed by constants and simple variables in program. 
• Space needed by dynamically allocated objects such as arrays and class instances.  
• Environment stack space: The environment stack is used to save information needed to resume execution of partially completed functions.  
• Instruction Space: The amount of instructions space that is needed depends on factors such as:  
• The compiler used to complete the program into machine code.  
• The compiler options in effect at the time of compilation  
• The target computer.

                        Space Complexity S(P)= C + SP(I)  

        Fixed space requirements(C) independent of the i/p and o/p  

• Instruction space.  
• Space for simple variables, fixed size structured variable, constants. 

        Variable space requirements SP(I) depend on the instance characteristics I  

• Number, Size, values of inputs and outputs associated with I. 
• Recursive stack space, formal parameters, local variable, return address.

2. Explain Quick Sort with Example.

Answer: Quick Sort is also based on the concept of Divide and Conquer. Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value. Quick sort is a fast sorting algorithm used to sort a list of elements.

It is also called partition-exchange sort. This algorithm divides the list into three main parts:

1. Elements less than the Pivot element
2. Pivot element(Central element)
3. Elements greater than the pivot element

Pivot element can be any element from the array, it can be the first element, the last element or any random element.

In Quick sort algorithm, partitioning of the list is performed using following steps...

• Step 1 - Consider the first element of the list as pivot (i.e., Element at first position in the list). 
• Step 2 - Define two variables i and j. Set i and j to first and last elements of the list respectively. 
• Step 3 - Increment i until list[i] > pivot then stop. 
• Step 4 - Decrement j until list[j] < pivot then stop. 
• Step 5 - If i < j then exchange list[i] and list[j]. 
• Step 6 - Repeat steps 3,4 & 5 until i > j. 
• Step 7 - Exchange the pivot element with list[j] element.

The following example shows that 54 will serve as our first pivot value.

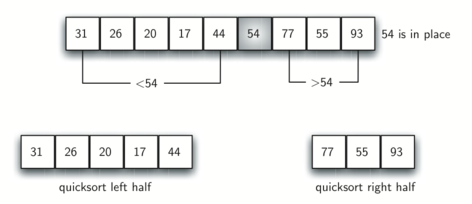
Partitioning begins by locating two position markers—let’s call them leftmark and rightmark—at the beginning and end of the remaining items in the list. The goal of the partition process is to move items that are on the wrong side with respect to the pivot value while also converging on the split point.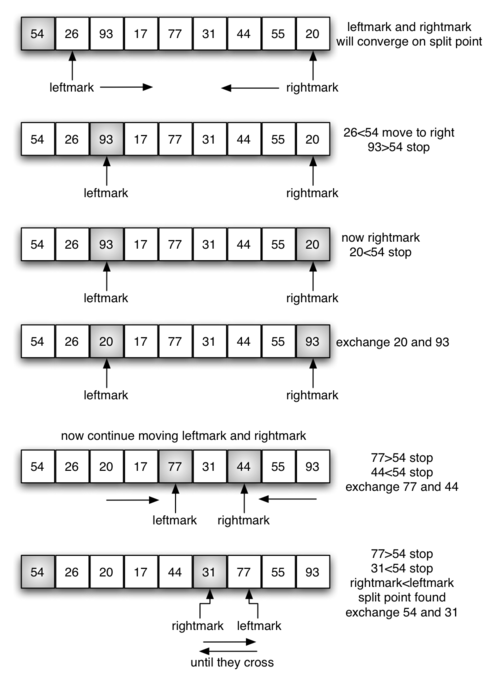

 

At the point where rightmark becomes less than leftmark, we stop. The position of rightmark is now the split point. The pivot value can be exchanged with the contents of the split point and the pivot value is now in place. In addition, all the items to the left of the split point are less than the pivot value, and all the items to the right of the split point are greater than the pivot value. The list can now be divided at the split point and the quick sort can be invoked recursively on the two halves.

 

Q. Write an algorithm for linear/sequential search. Also state its different variations.

Answer: Linear search is a very simple search algorithm. In this type of search, a sequential search is made over all items one by one. Every item is checked and if a match is found then that particular item is returned, otherwise the search continues till the end of the data collection. The search in Linear Search starts at the beginning of an array and move to the end, testing for a match at each item.

The sequential search is used whenever the list is not ordered. Generally, you use this technique only for small lists or lists that are not searched often.  In the sequential search, we start searching for the target at the beginning of the list and continue until we find the target. This approach gives us two possibilities: either we find it reach the end of the list.

Algorithm:

Linear Search ( Array A, Value x)

    Step 1: Set i to 1
    Step 2: if i > n then go to step 7
    Step 3: if A[i] = x then go to step 6
    Step 4: Set i to i + 1
    Step 5: Go to Step 2
    Step 6: Print Element x Found at index i and go to step 8
    Step 7: Print element not found
    Step 8: Exit 

Variations on Sequential Searches

Three useful variations on the sequential search algorithm are: 

1. the sentinel search
2. the probability search, and 
3. the ordered list search.

Read More